

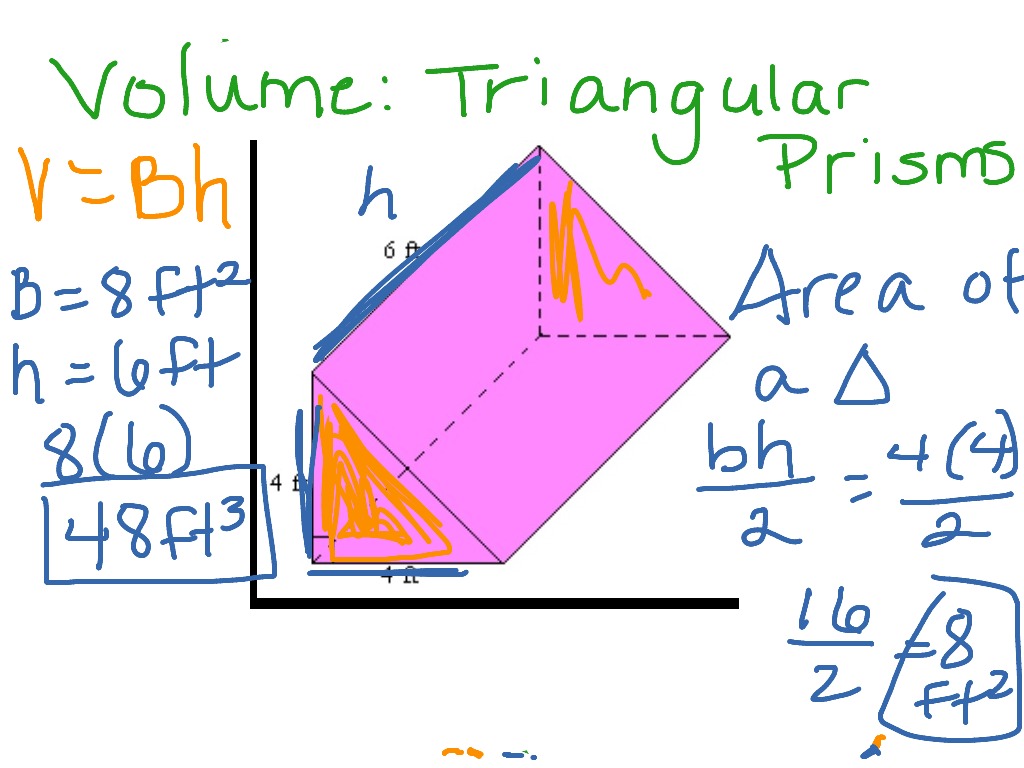
Students should see that the volume of a triangular prism can be determined by finding the area of the trianglular cross-section × length of the prism (1/2 bh × length).Įmphasise that the part of the formula 1/2 bh, refers to the base and the height of the triangular face and not the height or length of the prism.Īsk students to find a partner for this activity and provide them with a Note: it may assist students if the triangular prism is rotated or redrawn to allow them to see that the shape of the cross-section is a triangle.
Provide each student with 1 cm isometric drawing paper. What terminology they may not understand in that definition and provide Identical ends, straight sides and the same cross-section. Introduce prisms to students as 3-dimensional shapes that have Them to identify and find the area of the cross section rather Depending on the rotation of the shape the front face The area of the ‘front face’ and multiply this by the length or Of cross-section first they will be able to calculate theĪ common misconception may arise if students are told to find Two hexagonal prisms are the same volume but are Whether the student ‘see’ the length or the height.Į.g. On the rotation of the shape will determine The cross section is, find the area of it and then

Introduced as area of the cross section × length The cross section will be the same shape as the identical ends of the prism. Show how the cross section must be identical along the length (or height) of the shape.Īll these shapes are triangular prisms as they have identical triangular ends, straightĮdges and a uniform cross section. Rotations of the shape, so students become familiar with what is required to call a shape a When introducing new prisms such as a triangular prism show a variety of drawings and This formula only applies to rectangular prisms. Showing a justification for the formula will support student understanding that Rectangular prism made from 1 cm cubes or drawing one on a computer program such as Clarify with students how this formula is established by showing a Students may be familiar with the formula length × width × height to find the volume ofĪ rectangular prism. Prisms are three-dimensional shapes with identical ends that can be cut into identicalĬross sections all along their length or height. To develop formulas to calculate the volume of other prisms such as triangular prisms. The volume of a rectangular prism from ( VCMMG259). At this level, students will continue to develop their understanding of volume and finding


 0 kommentar(er)
0 kommentar(er)
